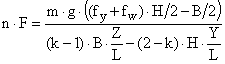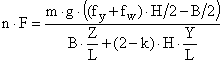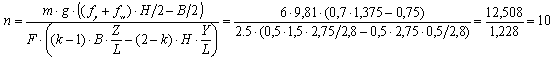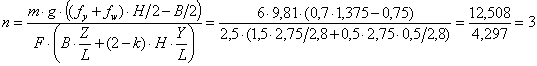2 Conventional rules and calculation methods |
[German version] |
2.2 Tie-down lashingTie-down lashing is conventionally treated for the most part such that only the vertical component of the pre-tensioning force is regarded either as enhancing friction or as increasing tipping stableness. Tie-down lashings generally do not have a horizontal lashing angle and are moreover virtually always applied in the transverse direction of the vehicle. 2.2.1 Securing against slidingSource [1] provides the sliding balance in the notation agreed above:
The balance may be solved to find n or F. A minimum pre-tensioning force is recommended for F, but it should not exceed 50% of LC. In the case of one-sided pre-tensioning, it is recommended initially to apply a higher force on the tensioning side so that, on equalization during the journey, the overall loss of pretension is not so high. No k-factor for friction losses during pre-tensioning is provided. The coefficient of dynamic friction is used for m. Source [2] adopts this approach, but in the case of one-sided pretension uses the k-factor which replaces the factor 2 (two legs to be tied down per string of lashing).
In the case of one-sided pre-tensioning, k = 1.5, in the case of two-sided pre-tensioning k = 2. The coefficient of dynamic friction is likewise used. In this approach, the two different horizontal components of the lashing-loops are disregarded. The difference between these forces could be introduced into the balance. The two forces amount to: Pre-tensioning side: Source [3] again turns away from the k-factor, but does introduce a safety factor fs = 1.1, which increases the necessary pre-tensioning force by 10%. The balance reads:
This agreement corresponds to a k-factor of 1.82. The reason stated for the safety factor in [3] is, however, not pre-tension loss by friction but instead calculation uncertainty. Source [3] moreover contains a sliding balance for the combination of tie-down lashing and blocking, again disregarding the load-bearing behavior of the two different securing means. 2.2.2 Securing against tippingSource [1] interprets the effect of the tie-down lashing as increasing the normal force onto the loading area, which increases the stabilizing moment with the half breadth as lever. Horizontal force components of the tie-down lashings here cancel each other out.
A similar formula is stated for the longitudinal direction, which however assumes longitudinally oriented lashing loops. Securing effects against tipping in the longitudinal direction by transverse tie-down lashings are not addressed. Source [2] treats the forces on the two sides of the cargo unit separately in the tipping balance and assumes the less favorable case in which the external force acts towards the pre-tensioned side. The expanded balance in the agreed notation reads:
If this balance is solved to get n × F, the following is obtained:
This formula for determining the necessary amount of securing has the unfortunate characteristic that, on the right-hand side, the denominator of the fraction may readily assume a value of zero. This gives rise to a result tending towards infinity on the left-hand side. If the denominator is equal to zero, then a combination of the variables B, Z, H and Y is present in which each further added tie-down lashing cancels out the vertical component, which increases tipping stability, due to the difference between its horizontal components, i.e. it has no effect. Anticipating section 3, it should be noted at this point that "permitting" a small offset, shift or tipping of the cargo unit under the external load reverses the forces. The balance then reads:
Once solved for n × F, the following is obtained:
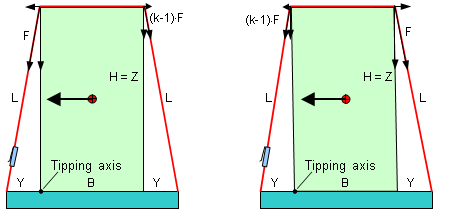
The difference in the results is demonstrated with an example. The values are: H = Z = 2.75 m, B = 1.5 m, Y = 0.5 m, L = 2.8 m, F = 2.5 kN, m = 6 t
Figure 12: Tipping balance according to source [2] on the left; alternative on the right According to source [2] on the left in Figure 12, 10 tie-down lashings are required for securing against tipping. If the calculation is performed with changed belt tensions as on the right in Figure 12, 3 tie-down lashings are enough. In this case too, the distribution of belt tensions corresponds to the decline in force due to friction at the top edges of the cargo unit. Elongation of the belts as a result of the slight shift of the cargo unit and the favorable increase in force has again not been taken into account in this comparison.
If the breadth B is reduced to 0.5 m, the number of tie-down lashings required according to the calculation in source [2] tends towards infinity, while taking a small movement of the cargo into account results in 7 tie-down lashings. Source [3] no longer uses the k-factor and so avoids the unfortunate calculation for securing against tipping. The approach from source [1] is adopted with the following modifications:
Source [3] additionally contains a calculation approach which tests the compacting action of tie-down lashings on a group of tall, narrow unit loads standing adjacent one another with regard to securing against tipping. This approach may be regarded as pointing the way towards the computational evaluation of compaction measures. |
|
Top of page
| Contents
| |