4.4
Securing against sliding in the transverse direction by slack tie-down lashing
This example is intended to demonstrate
that a tolerable cargo movement may also reestablish the securing effect of
slackened tie-down lashings in the transverse
direction. The same circumstances as in the preceding example are used for this
purpose.
The external force is determined as
conventionally agreed.
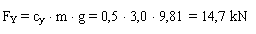
Conventional assessment of the securing against sideways sliding:
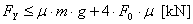
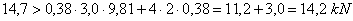
According to the conventional assessment,
securing is not adequate, with a shortfall of a good 3%. Here too it is
subsequently assumed that the pretension F0 in the tie-down lashing
has been lost due to the cargo units moving closer together.
Unlike in the
preceding example, where the movement distance selected was the DX value at which the belts still just grip the surface of
the cargo by friction, in this example the movement distance DY to be assumed was to be determined on the basis of the
geometric conditions of the loading area.
The cargo package has
a breadth of 2.4 m. At an assumed net breadth of the loading area of 2.5 m and
with initially central loading, the pallets may slip by 5 cm to the side before
coming into contact with the sidewalls. Racking (shear deformation) is
additionally assumed, in which the upper edges of the units are pulled a
further 10 cm to the side.
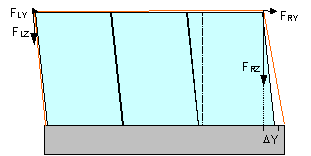
Figure 21: Cargo sliding and racking DY in
Querrichtung
The lengthening of
the belts arising from these movements is calculated:
| Initial length of the external parts of the belt: | 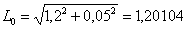 m m |
| New length on the right: | 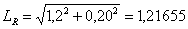 m m |
| New length on the left: | 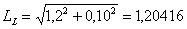 m m |
| Change in length: | 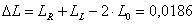 m m |
This change in length
results in force being created in the belt, which is distributed such that the
force FR acts in the right-hand vertical part of the belt, while
forces reduced by Euler’s friction losses act in the horizontal central part
and the left-hand vertical part. The individual changes in length must again
correspond to the total change in length. Change of direction on the right
amounts to a = 81° = 1.40 rad, while change of direction on
the left amounts to b = 95° = 1.66 rad. The coefficient of friction mL = 0.25
applies as in the preceding example.
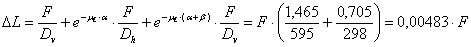
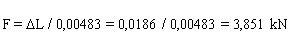
FR = 3,851 kN
with FRY = 0,60 kN and FRZ = 3,80 kN accordingly acts in the right-hand part of the belt
FL
= 0,465 × FR =1,791 kN with FLY = 0,16 kN and FLZ
= 1,78 kN acts in the left-hand part of the belt
The balance is completed with these values:
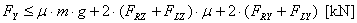
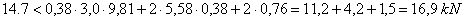
The balance is achieved with a surplus of
15%, any possible retention forces arising from the edge of the loading area
having been disregarded. This example confirms that a slight cargo movement can
compensate the complete loss of pretension. However, it must not be concluded
on this basis that pre-tensioning is unimportant. Instead, the actual, more
probable mode of action of a tie-down lashing should be pointed out, which does
not correspond to that represented in the conventional approach to calculation.
The conventional approach to calculation clearly does not adequately model the
physics to be applied in this case.
It is not yet possible to state the
extent to which the conventional approach to calculation may need to be modified on this basis.
|