4.3
Securing against sliding in the longitudinal direction with slack tie-down lashing
This example is intended to demonstrate
that a tolerable cargo movement may re-establish the securing effect in the
longitudinal direction of a transverse tie-down lashing,
even if the pretension has first completely disappeared due to settling of the
cargo.
Three loaded pallets each of a mass of 1.0 t are placed side by side on
the loading area and are tied down with two belts. The dimensions of the units
are 1200 x 800 x 1200 mm. The complete package has a height h of 1.2 m and a
breadth b of 2.4 m.
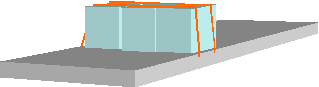
Figure
19: Tie-down lashing of box pallets
The belts run virtually vertically on the
external sides. At the beginning of the journey, the belt pretension amounts on
average to around F0 = 2 kN. The coefficient of friction relative to
the loading area is assumed to be m = 0.38 and that between the belts and cargo
to be mL = 0.25. This example solely
investigates securing against forward sliding.
The external force is determined as
conventionally agreed.
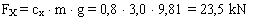
Conventional assessment of the securing against forward sliding:
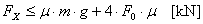
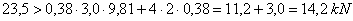
According to the conventional assessment,
securing is not adequate, with a shortfall of just about 40%.
Taking account of cargo movement:
In order to simplify the following
presentation, it is assumed that the pretension has declined to zero by the
three pallets having moved closer to one another. If the cargo is permitted to
shift forward in the event of an extreme load, belts on the top of the cargo
are dragged along without slipping until an equilibrium is reached between the
longitudinal component of the belt force FX and friction on the top
of the cargo FZ × mL. The resultant maximum movement
distance is calculated:
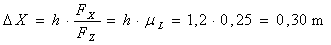
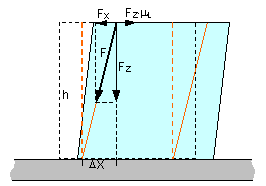
Figure
20: Cargo sliding and racking by DX in the longitudinal direction
This distance may be made up of the
sliding of the pallets and shear deformation.
The belts have lengthened in this state by the amount DL.
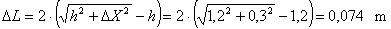
Lengthening results in force being
developed, but this is not uniformly distributed over the length of the belt.
The horizontal central part maintains a force which is reduced pro rata with
Euler’s friction losses at the edges relative to the force in the external
parts of the belt.
Each belt has an LC = 25 kN and an
elongation of 3.5% when LC is reached. The spring constant of the vertical
parts of the belt amounts to Dv = DF / DL = 25 / (0.035 × 1.2) = 595
kN/m, that of the horizontal parts of the belt only Dh = DF / DL = 25 / (0.035 × 2.4) = 298
kN/m. On this basis, the individual changes in length, which must add up to the
total change in length DL, may be determined with the initially unknown force F in the
external parts of the belt.
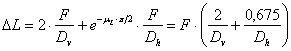
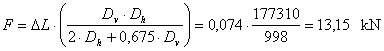
The belts thus reach a force in the
external parts of a good 13 kN on both sides. The horizontal central parts just
about reach 9 kN. The longitudinal and vertical components of the external
forces are calculated for the sliding balance.
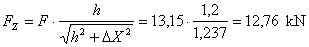
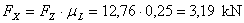
These values are used to make up a sliding balance.
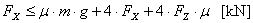
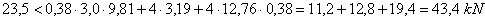
The balance is amply met with a surplus
of just about 85%. The cargo will in fact thus not have to slide or distort over the entire 30 cm in order to reach an equilibrium of
forces. This example is an impressive demonstration of the securing potential
which can be obtained from limited cargo movement. The question as to whether
the middle unit remains secured by friction relative to the other two external
units and to the loading area is left unanswered here.
|