1.1
Full braking
Full braking is the greatest load to
which a forward securing arrangement is exposed. Recent developments in the
field of truck tires, coupled with modern brake systems and asphalt roads,
permit braking deceleration values that are perfectly capable of approaching
0.8 g
(1).
Other factors, such as the distribution of axle weights, also play a role in
this context.
The connection between the loading area
of a truck or semitrailer and the tyre footprints is not rigid but resilient,
which means that the inertial force of the cargo does not follow directly from
the braking deceleration, but instead initially brings about a forward tilting
of the loading area. This "pitching angle" is not at a steady state
throughout full braking, but has pitching oscillations superimposed on it. The
amplitude of the pitching oscillations is very highly
dependent on buildup time, i.e. the time taken for the braking force to increase
to its full value.
During full braking, the following forces
act forwards on the cargo in the coordinate system of the loading area
(parallel to the loading area):
- inertial force component from the braking maneuver,
- downhill force (weight component) arising from
the geodetic inclination of the loading area (pitching angle and gradient of
road),
- inertial force arising from tangential
acceleration from superimposed pitching oscillation.
The normal force acting from the cargo on
the loading area is generally reduced by two causes, namely, as a result of the
inclination of the loading area, by the
- upwardly directed vertical component of the inertial force,
- reduced normal component of the weight-force.
The upwardly
directed vertical component of the inertial force, and the reduced normal force
arising from the geodetic inclination of the loading area reduce both the
friction relative to the loading area and the moment of stableness of a cargo
unit.
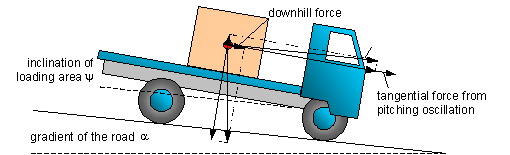
Figure 1: Full braking on downward sloping road
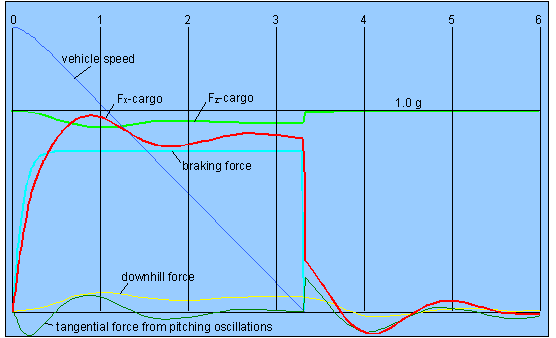
Figure 2: Full braking on a level road from 90 km/h with 0.8 g braking deceleration
and
0.3 s buildup time; stopping distance = 42.9 m
Figure 2 shows the numerical solution of
the equations of motion over a period of 6 seconds. The forces acting on the
Cargo have been converted into units of g. The vehicle is stationary after
approx. 3.3 seconds.
The truck is loaded in such a way that,
at 0.8 g deceleration, a steady-state pitching angle of 4° is obtained. The
maximum pitching angle after 0.9 seconds amounts to 5.5° as a result of the
superimposed pitching oscillation. This oscillation is strongly damped and
largely subsides by the time the vehicle is at a standstill, but is re-excited
by the familiar jerk at the end of the braking maneuver.
The maximum longitudinal load on the
cargo at 0.9 seconds amounts to 0.98 g, at which point the normal force has
simultaneously declined to 0.92 g.
Numerous further simulated full braking
maneuvers at other speeds, uphill and downhill road gradients and other vehicle
types (e.g. semi trailer with a smaller pitching angle) reveal similar
profiles. The following general conclusions may be drawn:
- Calculating on the basis of braking force transfer corresponding to
0.8 g, cargo securing must be designed for just about 1.0 g, because the
downhill force from the pitching angle plus the tangential force from the
superimposed pitching oscillation add about 0.2 g.
- Full braking from lower initial speeds results in only
insignificantly more favorable results. Only at speeds of below 15 km/h may it
happen that the vehicle is already stationary before the maximum longitudinal
force has been reached.
- Semi trailers, which are assumed to have half
the pitching angle, experience approx. 3% lower longitudinal forces and a 4%
lower reduction in normal force. The outcome is no more favorable than this
because the pitching oscillation period simultaneously becomes shorter and the
amplitudes of the pitching oscillations are only insignificantly smaller than
in a vehicle with a 4° steady-state pitching angle.
- The more rigidly is a loading area mounted, i.e.
the less it responds to deceleration with a pitching angle and with pitching
oscillations, the closer the longitudinal force acting on the cargo
approximates to the pure inertial force from the braking deceleration.
- Gentler braking maneuvers with buildup times of
longer than 2 seconds result in virtually no superimposed pitching oscillations.
Calculating on the basis of 0.8 g maximum braking deceleration, the only
further allowance which need be made is for the parallel component of the force
of gravity from a steady-state pitching angle. The allowance is obtained from
the sine of this angle.
- On full braking uphill from a speed of 50 km/h,
the braking force is increased by the backward downhill force and, as a result,
the braking distance is distinctly shorter than on a level road. The effective
pitching angle is, however, reduced by the rearwardly directed inclination of
the road, such that the difference in longitudinal force on the cargo is almost
equalized compared to the situation on a level road. Under the selected
conditions according to Figure 2, the cargo should be secured against acceleration
of 0.99 g.
- On full braking downhill from a speed of 50
km/h, the longitudinal force on the cargo is somewhat smaller than in the event
of full braking on a level street. The effective braking force is smaller and
the braking distance greater. The downhill force is, however, increased by the
inclination of the road. Under the selected conditions, the cargo should be secured
against acceleration of 0.96 g.
- Calculation methods for dimensioning
longitudinal cargo securing should take suitable account of the decrease in
normal force (weight).
|


