| Photo of the month – January 2015 |
[German version] |
Recipe
Some of our readers may well be thinking to themselves that we are more than a little late with Christmas recipes. But we can put your minds at rest. Our column is still about load-securing, and we intend it to stay that way. In this case, the recipe we are talking about describes what is, in our opinion, an extremely simple calculation method for dimensioning direct lashings used for securing loads.
When the police arrived at the "scene of the accident", the vehicle, a drop-deck trailer carrying a telescopic forklift truck, was already standing on the hard shoulder. It was plain to see that the two rear load-securing chains had snapped:

Figure 1 [Wolfgang Jaspers]
An initial inspection of the vehicle revealed that the load, a telescopic forklift truck with a weight of 14,000 kg, had slipped forward slightly (or perhaps it had even rolled), but had not reached the gooseneck, so that neither the load nor the vehicle were damaged:

Figure 2 [Wolfgang Jaspers]
After the police had escorted the vehicle from the motorway extremely carefully, it was possible to have a look at it without risking life and limb:

Figure 3 [Wolfgang Jaspers]
To start with, the load-securing material was inspected. In this case, chains had been used with a lashing capacity (LC) of 4000 daN each:

Figure 4 [Wolfgang Jaspers]
Figure 5 below is puzzling. On the load-securing point, you can read "LL 3,850", and we assume that the missing unit is "daN". This is followed by "SWL 12 t":

Figure 5 [Wolfgang Jaspers]
These specifications alone are simply confusing. SWL stands for "Safe Working Load" and is used for lifting gear such as cranes, slinging equipment, slinging points etc. A safety factor of four must be used in calculations for lifting operations and a safety factor of two for lashing operations. We could stick our necks out and assume that LL could perhaps stand for "Working Load Limit" and then try to establish some kind of a relationship between these two numbers, i.e. approximately 4 tonnes and 12 tonnes. The ratio is 3:1, not 2:1 as we might expect on the basis of the regulations governing lifting and lashing. So this assumption doesn't help us.
It is also noteworthy that the specifications for lashing and for lifting are both indicated on this load-securing point. As we know, this is not permitted. The reason for this is relatively simple: Load-securing points are often overloaded. This may be because some of the lashing equipment is loose and a jolt during transport causes the equipment to be subjected to a sudden load. Alternatively, it could be because vehicles rock and oscillate on the suspension and tires. Rocking, oscillating motion such as this can often be seen when construction vehicles are being transported. The result is that the load-securing equipment is constantly being subjected to loads and then relieved. Consequently, load-securing points and the load-securing equipment can become overloaded. Because nobody can see with the naked eye whether the material has ever been loaded beyond its capacity, it is absolutely forbidden to use load-securing points for lifting. The reason is that the safety factor for lifting is twice as high as for lashing, and the failure of a slinging point would have immediate consequences.
We would like to see unambiguous labeling on load-securing points such as these:
- " They are suitable for lashing, with a value followed by LC, or
- " They are suitable for lifting, with a value followed either by SWL or WLL (Working Load Limit).
An additional label that clearly indicates which point is suitable for lifting and which for lashing would provide an additional level of safety and clarity for users. When we contacted the manufacturer, we found out that these load-securing points were not factory fitted. We presume that an inventive owner had been doing some DIY on this telescopic forklift truck. Even though it is laudable that people have given some thought to ways of securing their load, this example shows that such measures have to be thought through properly.
The officers at the scene wanted to check how the chains had been attached and whether the load-securing measures were adequate. To do this, the telescopic forklift truck was moved backwards sufficiently to tension the front chains again. Although it was not possible to precisely reproduce the original pre-tensioning forces and angles, we shall ignore this fact for the purposes of our rough calculation:

Figure 6 [Wolfgang Jaspers]
The recipe
The recipe really is as easy as pie. Our diagram also shows a number of angles:
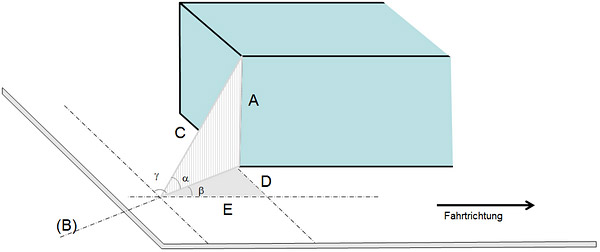
[GDV]
All around us, and especially in the formulas for calculating load-securing measures, we see angle functions. But angle functions are ultimately nothing more than ratios between the sides of triangles. And this means that we can happily ignore the angles indicated by alpha, beta and gamma in the diagram.
In order to determine the ratios between the lengths involved, the first thing is to measure the distances that are relevant for load-securing purposes. These are the distances marked A, C, E and D. The distance B is not needed! The distances must be measured between the point at which the lashing equipment is attached to the load and the point at which it is attached to the vehicle. If the equipment is passed over the edge of the loading bed in order to secure it to the underside of the bed, the measurement is taken to the point at which it is deflected over the edge of the bed. This means that the effective length of the load-securing equipment is measured in the relevant direction. These distances represent the effect of the load-securing equipment in each direction, and we only have to determine the ratios between them. This is done by dividing the effective longitudinal component (E) by the length of the load-securing equipment. Thus, we divide the length E by C to give a factor that is always less than one, because the length C is always the greatest length. Now, all we have to do is multiply this factor by the LC value for the load-securing equipment to obtain the precise value for the longitudinal effect of the load-securing equipment. We can perform exactly the same calculation for the distances D and A.
In the case of the distance A, there is a further issue in that it also acts as a tie-down lashing. We shall look at this in detail below.
Because it is usually possible to measure these distances very accurately, this "recipe" is considerably more accurate than any method that involves measuring angles. If, for any reason, one of the components cannot be measured because of the shape of the load, this can be overcome by measuring a specific distance, for instance one meter, along the actual load-securing equipment. This distance is then marked with a chalk mark. A plumb line (which can easily be made from a nut and a piece of tape) is then used to drop a perpendicular to the loading surface. Of course, it is necessary that the vehicle is not on a slope or tilted for this to work. Another chalk mark is made at the bottom of the plumb line, and the relevant distances E, D and A can then be measured from this point. Although these measurements result in shorter lengths, the ratios between them remain identical. If you measure exactly one meter along the load-securing equipment, the advantage is that the lengths measured correspond directly to the factors, since you only have to divide by 100 cm. Example: If the distance E is measured as 60 cm, and if we have put our mark 100 cm along the load-securing equipment, we divide 60 by 100 to give the factor 0.6. If the distance was 40 cm, this would give a factor of 0.4 and so on. If the factor is 0.6, we only need to multiply this by the LC of the load-securing equipment, e.g. 2000 daN. In this case, the longitudinal securing effect would be (0.6 x 2000 daN) = 1200 daN. And that's all there is to the recipe. Which is why we have called it a "recipe".
To visualize exactly how this works, consider the following:
Let us secure the load-securing equipment to the bottom corner of the load, effectively placing the load-securing equipment directly on the loading surface, and pass it backwards at right angles to an imaginary load-securing point situated at a perfect position. With this arrangement, there are no angles gamma, alpha or beta, and there is no vertical component or lateral component. If you now measure the distances C and E, they will be the same. For instance, 175 cm. If you now divide the 175 cm by 175 cm, this results in a factor of 1. If we now dogmatically apply the approach dictated by the recipe we would have to multiply the LC of the load-securing equipment by the factor 1. In other words, the load-securing equipment acts 100 % against movement in the direction of travel, i.e. with 2,000 daN in our example. If we take the same example and move the load securing point just 10 cm up, leaving all the other parameters the same, C would be 175.3 cm rather than 175 cm and there would be a very small vertical component.
And we could do the same thought experiment for the distance D. It would make no sense to do so for the distance A, as this lashing would be a tie-down lashing. Any lashing used on the load that lies between a right angle longitudinally and a right angle laterally has E, D and A, components in the same proportions as the ratios between the distances. And that is the end of it. And we haven't even mentioned the words tangent or sine. Many people ask why the distance A must also be divided by the distance C and this factor then be multiplied by the LC. After all, the pre-tensioning force should not exceed 50 % of the LC. The following conditions apply to this case: For a direct lashing to act, the load must (in our case) slip forward slightly. If we imagine the load slipping forward sufficiently that the maximum lashing capacity is reached, the direct lashing does not at that moment act only with its E and D components, but also with the vertical component that equates to a tie-down lashing. Depending on the length A, these tie-down lashing forces can be considerable, so we do not wish to exclude them from our recipe. Of course, it is important that the vertical component only takes effect in combination with friction. Thus, if a vertical component of just 400 daN is identified, we then have to multiply this by the coefficient of friction. But let us return to the case in hand.
In our example, the distance C was measured as 126 cm:

Figure 7 [Wolfgang Jaspers]
The distance E, or the longitudinal component, in our example was measured as 51 cm:

Figure 8 [Wolfgang Jaspers]
And the distance D was measured as 61.5 cm:

Figure 9 [Wolfgang Jaspers]

Figure 10 [Wolfgang Jaspers]
The distance A was 93 cm. (Unfortunately, we have no photograph to show this.) Dividing out the individual distances, gives the following results:
The distance E/C gives a factor of 0.4.
The distance D/C gives a factor of 0.49 and
the distance A/C gives a factor of 0.74.
If these factors are multiplied by the lashing capacity of 4000 daN, one chain will deliver a securing force of 1600 daN longitudinally, 1960 daN laterally and will provide a vertical component of 2960 daN. If we use a coefficient of friction μ of 0.3, the 2960 daN must then be multiplied by this coefficient μ of 0.3. This still results in a securing effect of 888 daN with one chain.
With respect to the longitudinal direction, this results in the following:
In the direction of travel, with a load weighing 14,000 kg, acceleration of 0.8 g and an assumed coefficient of friction μ of 0.3, it is necessary to provide a total securing force of 7000 daN. Each of the chains, which were originally exactly the same length, provided 1600 daN, making a total of 3200 daN. The vertical component gives us a value of 888 daN for one chain and 1776 daN for both chains. This all adds up to 4976 daN of securing force. This represents a shortfall of 1624 daN securing force. But if we were able to assume a coefficient of friction μ of 0.4, we would only require 5600 daN of securing force. This increase in the assumed coefficient of friction would also give us an additional securing force of 592 daN through the vertical component. This would give a total (longitudinal) securing force of 5568 daN. This means that there is still a shortfall of 32 daN before the forklift truck is secured in accordance with regulations.
Load-securing:
Now we are justified in asking why the load-securing arrangements did not restrain the load. After all, the shortfall of 32 daN should easily have been taken up by the spare capacity in the load-securing equipment.
Observant readers may have noticed that we have not spent any more time discussing the load-securing points on the bed or on the telescopic forklift truck. To avoid this month's column becoming too lengthy, we have restricted ourselves to the "facts", and it is an established fact that the chains failed and that the load-securing points on the vehicle and on the load did not.
Let us go back to Figure 3 and have a closer look at the friction: Here we see that the telescopic forklift truck is standing slightly to the left on the bed. This could have happened as a result of the right-hand chain failing first, but because the truck is more or less aligned with the trailer and still positioned slightly to the left, it is possible that it was originally loaded in this position. If we now have a look at Figure 6, we can see that, although the vehicle had already been moved back by this time, the wheels are partially on the painted steel. At this point, the friction is certainly lower than on the ridged mesh. Given that the tires and the loading surface are quite clearly clean, we believe that a coefficient of friction of at least 0.4 should have been perfectly plausible.
Of course, we also asked ourselves whether the vehicle may have rolled rather than slipped. When we asked the manufacturer, they assured us that the brakes can only be released when the engine is running and that as soon as the engine is turned off, the vehicle is braked automatically. So this does not appear to be the solution. The load-securing equipment was in pristine condition and the load-securing points (we have already talked about the ones on the forklift truck) were not faulty. All of which leads us to the conclusion that the chains were slack when the jolt occurred during braking. If the chains (or other load-securing equipment) are slack at the moment the load slips, the resulting force can be of such a magnitude that even the safety margin in the load-securing equipment is no longer sufficient to restrain the load. The safety margin inherent in the load-securing materials is absolutely necessary to absorb any movement in the load, which must, as we described above, slip into the chains to tension them up to their LC. And the load is still moving when the lashing capacity has been reached. But this kinetic energy must also be absorbed by the load-securing equipment (although current guidelines make no mention of this; kinetic energy is simply ignored in the guidelines).
Suggestions for improvement:
So how can things be improved? Our recipe revealed that the longitudinal component E was the smallest component at 56 cm. But the load-securing equipment had an LC of 4000 daN in a longitudinal direction and less than 50 % of this was used. Longer chains attached further back on the vehicle would have considerably increased the securing effect.
The way in which the chains were attached to the telescopic forklift truck resulted in extremely steep angles. Steep angles are the nemesis of any load-securing equipment, as any vertical vibrations will always jolt the equipment. We do not know the extent to which this telescopic forklift truck is able to move on its suspension. But its balloon tires, designed for rough terrain, most certainly allow the truck to move. This is more than enough to allow the truck to gently sway and rock during transportation. And at each movement, the vertical component introduces a small jolt into the load-securing equipment. This is fatal for belts, and even more so for chains. This means that the smaller the vertical component, the better the load-securing equipment will be protected (only for direct lashings, of course). It would be best if vehicles such as these could be supported so that they are no longer resting on their suspension. We do not know whether the hydraulic rams designed to support the vehicle on rough terrain and while it is in use can also be extended on the loading bed. But this would prevent the load from oscillating as it bounces on its tires and/or suspension. In order to ensure that there is sufficient friction under these hydraulic rams, heavy-duty mats would need to be placed beneath them.
Once again, we return to the positioning of the chains, which is a key issue for us. If these chains had been attached as little as one meter further back on the vehicle, this would have resulted in a far larger longitudinal component. A longitudinal component of just 0.8 would have increased the securing force by 2800 daN without the need to use any additional load-securing equipment.
And a word about the pre-tensioning force: It is still common to hear people being instructed to tension direct lashings only hand-tight. Assuming that the load-securing equipment to the front and rear can be placed more or less symmetrically, it is certainly beneficial if the pre-tensioning force is as high as possible, provided that it does not exceed 50 % of the LC. This is because the telescopic forklift truck must have the freedom to slip a few millimeters or even centimeters forward to allow the chains at the rear to reach their full lashing capacity. At the same time, the front chains are relieved to a corresponding degree, which means that the forklift truck doubles the pre-tensioning force while slipping only half the distance.
Your load-securing columnists apologize for the length of this Photo of the Month. We wish you a healthy, successful and above all secure 2015.
Your Load Securing Team
Back to beginning
