| Photo of the month – March 2006 | [German version] |

Figure 1
Loading steel
This steel loading scenario was seen at the Miniatur-Wunderland model world in Hamburg. Our diminutive colleagues are in the process of securing steel sheet on a semitrailer.

Figure 2

Figure 3
Figures 2 and 3 show that the load securing relies on friction and tie-downs. Three tie-downs have already been attached and a fourth is being prepared.
What is being illustrated in the models can be seen day in, day out in loading bays throughout the world. The following worked calculation shows that a lot more than four tie-downs are required to secure a load of this type.
Calculation of the load securing required in the longitudinal direction (direction of travel) if tie-downs are used:
Three steel sheets have been loaded, each of which weighs 6 metric tons. It is only possible to speculate on the frictional forces which apply here. The bottommost steel sheet is resting on wooden planks. In this case, we can assume a coefficient of friction µ = 0.3 (metal on wood). The remaining steel sheets are stacked on top of each other without any further intermediate layers. In this case, the coefficient of friction is at best µ = 0.25 (metal on metal, dry). To simplify the calculation of the number of tie-downs required, we shall assume a coefficient of friction of µ = 0.3. Lashing belts with a lashing capacity (LC) of 2,500 daN are used to secure the load.
| Required total forward securing force (0.8 g, i.e. 80% of the load weight force): 18.0 metric tons x 0.8 g* = 14,400 daN | |||||||
| Frictional securing force: 18.0 metric tons x 0.3 g = 5,400 daN | |||||||
| Lacking securing force: 9,000 daN | |||||||
| Securing force of a tie-down lashing: Prestressing in straight line (normal ratchet) = 250 daN (0.1 x LC), prestressing in strapping** = 2 x 250 daN = 500 daN*** | |||||||
| The fact that the belts could not be passed at an angle of 90° from the lashing point to the edge of the load was disregarded for the purposes of this calculation. | |||||||
| Securing action of a tie-down lashing: securing force x friction coefficient = 500 daN x 0.3 = 150 daN | |||||||
Number of lashing belts required for tie-down lashing: lacking securing force divided by securing action per belt = 9,000 daN / 150 daN = 60 lashing belts!!!
|
The effort involved in this case can be reduced considerably by using a different securing method.
To start with, nonslip intermediate layers or a combination of square lumber dunnage and nonslip materials can be used to increase the friction. Also, direct securing of the load with loop lashings (V lashings) is also to be recommended – see Figure 4.
These steel sheets could have been entirely adequately secured by two loop lashings on each side, two loop lashings around the front end face and one loop lashing around the rear end face. The belts may have to be protected from sharp edges on the load by suitable means.
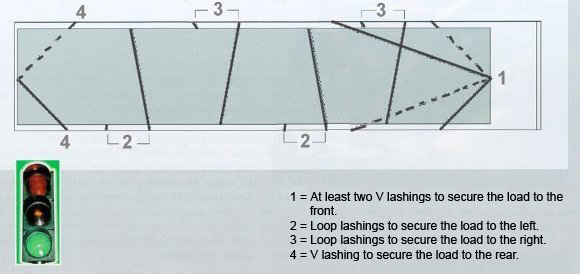
Figure 4
Calculation of the load securing required in the longitudinal direction when using loop lashings:
It is assumed that nonslip materials are used, giving a friction coefficient µ = 0.5. Lashing belts with a lashing capacity (LC) of 2,500 daN are used to secure the load. The load securing points of the vehicle have an LC of 2,000 daN. The smaller value must be used for calculation.
| Required total forward securing force (0.8 g, i.e. 80% of the load weight force): 18.0 metric tons x 0.8 g = 14,400 daN | |
| Frictional securing force: 18.0 metric tons x 0.5 g = 9,000 daN | |
| Lacking securing force: 5,400 daN | |
| One loop lashing attached to two load securing points provides a securing force of 2 x 2,000 daN = 4,000 daN. The angle of spread causes up to 10-20% of the securing force to be lost, with the result that in the worst case, 3,200 daN securing force is available per lashing. If two lashings are used, 6,400 daN securing force is available in total. |
Information and suggestions on the safe transportation of metal sheets can be found on pages 212 through 226 of the GDV Cargo Securing Manual.
Back to beginning
