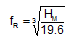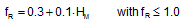1. Weather dependent load assumptions for cargo securing |
[German version] |
A reduction of load assumptions for navigating in restricted areas, accounting for the season of the year and the weather forecasts for the intended voyage, has been facilitated in principle in the Annex 13, but not explicitly specified. The need for a unified interpretation does not only result from a desirable cost reduction for cargo securing but also from occasional shipments of cargo units which are too sensitive against full scale accelerations and therefore require moderate transport conditions. Restricted sea areas or benign condition weather windows are generally distinguished by a less heavy seaway.
1.1 Significant wave height
The actual seaway in a specified area is usually denoted by the oceanographic term „significant wave height“ with the acronym HS. Figures of HS are usually part of ocean and coastal weather forecasts for relevant sea areas and for the time span of one or more days. HS is a statistical measure of wave height in a given wave spectrum and corresponds closely to the arithmetical mean of the upper third of wave heights in that spectrum. It further coincides fairly well with the prominent wave height estimated by an experienced local observer. The mathematical definition of HS implies, that
- 13.5% of all waves in the actual spectrum are higher than HS
- 1% of all waves are higher than 1.5 · HS
- 0.03% of all waves are higher than 2 · HS
- 0.01% of all waves are higher than 2.15 · HS
- waves higher than 2.2 · HS are classified as freak waves related to the actual HS
1.2 Long-term statistics
Another more long-term description of seaway conditions in a specified area is the so-called 20-year significant wave height. This height is much greater than the usual day to day figures of HS. It is a theoretical construct, derived from long term observations, and denotes a significant wave height that will be exceeded only once within 20 years in this area. Thus the 20-year significant wave height may be used as a yardstick to compare different sea areas in terms of general seaway severity. Examples of 20-year significant wave heights are:
| North Atlantic Ocean: | HS20year = 19.6 m |
| Mid North Sea: | HS20year = 11.9 m |
| Baltic Sea: | HS20year = 8.5 m |
The 20 year significant wave height of 19.6 m on the North Atlantic has been confirmed by repeated measurements of significant wave heights of this magnitude during the last years, results that have been published by the Danish Meteorological Institute DMI.
1.3 Long-term statistics
The increase of off-shore marine operations and sensitive ocean shipments during the past decades has gone along with research and wave data collection. One outcome of this effort is a calculation tool that permits to determine a probability based significant wave height for operational purposes. The results are available for a large repertory of sea areas and for an optional number of operation days in that area. This tool is published by DNV-GL in the standard DNV-GL-ST-N001.
The figures of significant wave heights obtained by this calculation tool do not necessarily coincide with those from meteorological institutes because they are matched to vessel response and allowable stress design in the first place, but they might be as well used as parameters in a unified interpretation of the allowance made by the Annex 13.
An extract of the world map shows the reference numbers of sea areas.
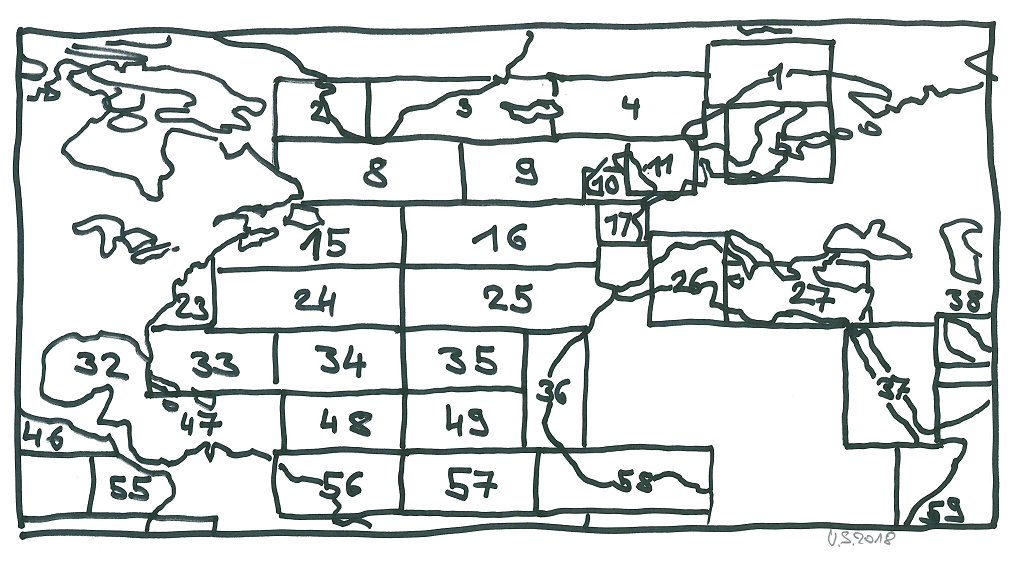
Figure 1.1: Extract of the world map of sea areas
1.4 Reduction of acceleration figures in moderate sea conditions
Although the Annex 13 offers a possible reduction of acceleration assumptions explicitly for operation in a restricted area, this must not necessarily be understood only in a geographic sense but should include time limited operation in a moderate sea state anywhere in the world. Then the predicted significant wave height may be the only essential parameter.
There are presently two different reduction models available. Both models provide a reduction factor for the accelerations when entering with the parameter HM, which is the greatest of all predicted significant wave heights HS along the intended sea passage.
The first model has been introduced in 1993 in Sweden as a national tool and later in 2011 included into the revised IMO Code of Safe Practice for Ships Carrying Timber Deck Cargoes (TDC Code). This model is also the basis for the acceleration levels presented for different sea area in the IMO/ILO/UNECE Guidelines for Packing of Cargo Transport Units from 1997 and also in the revised IMO/ILO/UNECE Code of Practice for Packing of Cargo Transport Units (CTU Code) from 2014.
The second model has been developed by the International Association of Classification Societies (IACS) in 2013 in the aftermath of the Lashing@Sea project. It has been based on measurements of accelerations on different vessels in identified sea states and on theoretical vessel response models.
The Swedish reduction model is represented by the formula for the reduction factor fR.
The constant 19.6 in this formula denotes the height of the twenty year significant wave in the Northern Atlantic Ocean. Figure 1.3 shows the graph of the formula together with numerous points of sample reduction factors showing the relations of measured accelerations to the calculated Annex 13 acceleration level.
The vast majority of measurements has been collected in sea states with HS-values not greater than 8 metres. There were, however, a few observations in greater wave heights. This may be explained by the limited number of ships operating in greater wave heights and by today’s weather routeing which enables to avoid such areas.
The Swedish model has been successfully used, not only by Swedish flagged vessels, in the Baltic and North Sea shipping, particularly in roro-ships and ferries with semi-standardised stowage and securing systems, and also in the Baltic timber trade. In lack of other models for reducing the accelerations to a reasonable level in modern shipping the model has been accepted by most Maritime Administrations and Classification Societies.
The IACS reduction model is represented by the formula:
This means there is no reduction, if the significant wave height is equal to or greater than 7 metres, while 0.3 will be the minimum reduction factor. Full scale measurements in sea states with significant wave heights of up to 7 metres appear to justify a more stringent reduction policy than offered by the Swedish model. This applies mainly for sea states with significant wave heights of more than 5 metres.
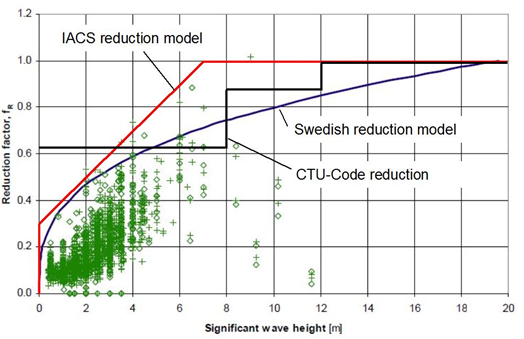
Figure 1.2: Swedish reduction model, IACS reduction model and CTU requirements
1.5 Unified interpretation of the „reduction clause“ in the Annex 13
The utilisation of a reduction factor would be simply its multiplication with the specific longitudinal, transverse and vertical forces obtained from the Annex 13 tables. The subsequent balance calculations for the prevention of sliding or tipping of the cargo unit in question would be satisfied with correspondingly less securing effort.
Another practical application of the reduction factor would be the preparation of tables or diagrams for a distinguished vessel in its Cargo Securing Manual. Such tables or diagrams would show the necessary securing effort in different stowage positions in the vessel, depending on the forecasted sea state in terms of significant wave height. This practice has been employed successfully for many years in the Baltic and North Sea trades.
At the time being it is still open, which of the two models or what compromise solution may be given the IMO recommendation status in the form of a unified interpretation of the reduction clause in the Annex 13. Whatever model is used, the essential parameter HM should be specified in terms of reliability, which may be made dependent on the prediction period and/or possible ports of refuge underway.
One possible solution may be to distinguish different modes of cargo transport according to the following:
- The assumed accelerations shall be taken from the Annex 13.
- The assumed accelerations may be reduced using the Swedish (TDC) model for vessels with standardized (excluding containers) and semi-standardized stowage and securing systems as well as for vessels carrying timber deck cargoes.
- For vessels carrying cargoes in a non-standardise mode of transport the assumed accelerations may be reduced according to the IACS model.
This solution should be complemented by a definition of the positive properties of standardised and semi-standardised stowage and securing systems in order to guarantee the appropriate world-wide application. Good Cargo Securing Manuals will contain this already.
| Top of page | Contents |